مهارت مدلسازي و الگويابي
1- الگويابي (پيدا كردن الگو)
الگوها خود را در موقعيتها و موضوعات طبيعي و روزمره نشان ميدهند. الگوها در رياضيات برجسته و شاخصاند؛ به طوري كه الگوهاي عملي و قابل استفاده، در حل مسئله رياضي قابليت اجرايي گستردهاي دارد. اين الگوها براي كودكان كودكستان و مدارس ابتدايي در زنجيرة مهرههاي رنگي، بلوكهاي (معكبهاي) اسباببازي و ضرباتي كه به ترتيب به يك طبل ميزنند، قابل شناسايي است. كودكان مدارس ابتدايي بايد الگوهاي عددي را در يك رديف مانند:
.... و 30و 25و 20و 15و .... و 6و 4و 2و 0 پيدا و مطالعه كنند. آنان ميتوانند الگوها را با عددهاي ديگر كامل كنند. در فعاليت زير، كودكان، الگوها را در طرحها و رنگهاي «پيراهن» بررسي ميكنند.
مسئله 1 الگوهاي «بلوز»
كودكي كه «بلوز» ساده و بدون يقهاي برتن كرده است، انتخاب كنيد، (بلوزي با خطهاي آبي و سفيد). از كودك بخواهيد الگوي بلوز را شرح دهد.
كودكان ديگري را كه الگوهاي مشابه «بلوز» دارند، انتخاب كنيد. از آنان بخواهيد الگوي «بلوز» خود را توضيح دهند.
از هر كودك بخواهيد، تصوير يك «بلوز» را بكشد و رنگآميزي كند.
توضيح دهيد كه چگونه ميتوانند به كمك حروف، الگوهاي «بلوز» را شرح دهند. الگوي يك در ميان «آبي- سفيد» با الگوي ….b- a- b-a-b-a و الگوي يك در ميان «آبي- سفيد- قرمز» با الگوي c-b-a-c-b-a قابل بررسي است. (رديفهاي باريك هر رنگ، كه رديفهاي كلفت را جدا ميكنند، قسمتي از الگو به حساب نميآيند. بنابراين الگوي بلوز فقط با رديفهاي پهن قابل تعريف است)
• الگوهاي حرفي مانند: a-b-c-d-a-b-c-d- ... a-b-c را روي كارتهاي «5×3» بنويسيد. به هر كودك يك كارت بدهيد. هر كودك بايد با مدادرنگي، الگوي روي كارت را رنگآميزي كند.
كودكان پايههاي تحصيلي بايد با الگوهاي پيچيده و انتزاعي كار كنند: فعاليتهاي زير، بررسيهاي چهار الگوي متفاوت را نشان ميدهد:
مسئله 2 الگوهاي حسابي
دنبالههاي متوالي حساي يكي از الگوهاي است كه بين هر عدد منظم و پايداري مشاهده ميشود. اعداد زوج ... و 4و 2و 0 از توالي حسابي شكل گرفته است. چون هر عدد كه با دو جمع شود، عدد زوج بعدي به دست ميآيد. (كودكان بايد اين مسائل را با استفاده از ماشين حساب حل كنند)
• رديف متوالي .... و 4و 3و 2و 1 را روي تخته بنويسيد. از كودك بپرسيد، عدد صدم در اين رديف، چه عددي است؟ (100)
• اولين اعداد فرد ... و 7و 5و 3و 1 را روي تخته سياه بنويسيد كودك بايد توالي اعداد را تشخيص دهد و نام چند عدد بعدي را بگويد.
• از كودكان بخواهيد، نام صدمين عدد در توالي با بگويند (199)
• چند عدد متوالي را به ترتيب روي تخته بنويسيد ...و 13و 10و 7و 4 كودك بايد نظم و ترتيب را در توالي تشخيص بدهد و نام چند عدد بعدي را بگويد.
• هر رديف از اعداد متوالي زير را روي تخته سياه بنويسيد و فعاليت را ادامه دهيد:
.... و 12و 9و 6و 3
... و 21و 15و 9و 3
• از كودكان نام صدمين عدد را در هر رديف بپرسيد.
• به كودكان كمك كنيد تا قاعدة تعيين هر عدد را در توالي حسابي، استنباط كنند.
الگوهاي عددي مشابه مسئله 2 در برنامة كامپيوتر قانون پادشاه قابل مشاهده است. دانشآموزان الگوهاي عددي شكل را بررسي ميكنند و با عبور از «قصر پادشاه» با آنها آشنا ميشوند. اين بازي به آنان امكان ميدهد با پيروي از قانون، به ايجاد عدد و بررسي الگوهاي خود بپردازد. بازيكني كه به «قصر پادشاه» برسد، مهارت و ورزيدگي خود را در الگوي نمونه معما نشان ميدهد.
الگوهاي دو مسئله بعدي با بررسي «ابزارهاي دست ساخت» معين ميگردد. در اولين الگو، صفحاتي مانند كارتهاي رنگي قابل استفاده است. در دومين الگو از معمايي به نام «برجهاي هانوي» استفاده ميشود. كودكان پايههاي سوم تا ششم ميتوانند الگوهايي در اين دو مسئله پيدا كنند. كودكان ورزيده پايههاي پنجم و اوايل دورة راهنمايي قادرند قانون دستيابي به اعداد گمشده را در هر توالي استنباط كنند.
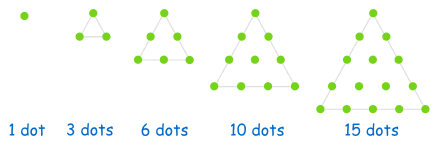
مسأله 3 اعداد مثلثي
اعداد مثلثي اولين مطالعة يونانيان علاقهمند به روابط بين اعداد و هندسه بود. مثلثهاي نقطهاي زير، چهار عدد مثلثي را نشان ميدهد.
• چهار عدد مثلثي اول را بنويسيد.
• تصوير عدد مثلثي بعدي را بكشيد. اين عدد را به فهرست اعداد مثلثي خود اضافه كنيد.
• فهرست اعداد مثلثي خود را بررسي كنيد و ببينيد آيا ميتوانيد الگويي براي آن طرح كنيد؟ هر الگويي را كه به دست آورديد، بنويسيد.
• سه عدد مثلثي بعدي را به فهرست خود اضافه كنيد.
• در صورت امكان، قانوني كلي (جامع) براي پيدا كردن عدد كل نقطههاي به كار رفته در مثلث با تعداد نقطههاي به كار رفته در هر ضلع بيان كنيد. قانون خودرا به صورت فرمول بنويسيد. از قانون خود براي پيدا كردن تعداد نقطههاي به كار رفته در مثلثي با 15 نقطه در هر ضلع استفاده كنيد.
مسئله4 برجهاي هانوي
برجهاي هانوي معمايي قديمي است كه حلقهها از يك قسمت به قسمت ديگر منتقل ميشود در تصوير، پنج حلقه در شكلي از سه رديف قرار گرفته است. مسئله اين است كه با كمترين حركت انجام شده پنج حلقه را به هر يك از قسمتهاي ديگر منتقل كنيد. شيوه حركت حلقهها به قوانيني مربوط ميگردد. حلقه بزرگتر هرگز نبايد روي حلقه كوچكتر قرار بگيرد و سپس حلقهها بايد مانند اول قرار بگيرند. (سومين ميله آخرين قسمت انتقال داده شدهي حلقههاست) مسئله: كمترين حركت انجام شده براي انتقال 5 حلقه كدام است؟
• براي حركت يك حلقه چند حركت لازم است؟ براي دو حلقه چه طور؟ سه حلقه چه طور؟ چهار حلقه چه طور؟
• آيا ميتوانيد از الگويي استفاده كنيد كه تعداد حركات 5 حلقه را تعيين كند؟
• فكر ميكنيد براي حركت شش حلقه به چند حركت احتياج داريد؟ براي هفت حلقه چه طور؟
• در صورت امكان، قانون كلي (جامع) براي پيدا كردن كمترين حركت انجام شده در انتقال n حلقه بيان كنيد. از قانون خود براي پيدا كردن تعداد حركت انجام شده با دوازده حلقه استفاده كنيد.
• قانون و پاسخهاي خود را با همكلاسيها مقايسه كنيد.
مسئله زير سرگرم كننده است. توالي رياضي رعايت نشده است و هيچ قانون كلي براي تعيين عدد گمشده ديده نميشود.
• مسئله 5 راز يك توالي رياضي
پنج عدد بعدي را در توالي زير تعيين كنيد.
...و 30و 24و 20و 18و 14و 12و 8و 6و 4و 3
يكي از فوايد اين مهارت در حل مسأله است.كشف الگو و رابطههاي بين داده هاي مسأله به حل آن كمك ميكند. الگويابي براي مسائلي مفيد است كه با استفاده از رابطهها و قواعد تكرارپذيري طرح ميشوند. گاهي كشف الگو همان حل مسأله است و در مواقعي پيدا كردن الگو راه را براي حل مسأله باز ميكند.
با استفاده از شكلها و عمليات مربوط به هر شكل، مجموع اعداد فرد 1 تا 25 چقدر ميشود (به عبارت ديگر، حاصل عبارت = 25+ 23+ ...+ 7+ 5+ 3+ 1 را پيدا كنيد).
همانطور كه در الگوي بالا ديده ميشود، مجموع عددهاي فردي برابر است با n2 كه در اين عبارت n عدد وسطي در آن دنباله است. در دنباله 5+3+1 عدد وسط 3 است پس: 9= 32= 5+3+1 و در دنباله 7+ 5+ 3+ 1 عدد وسط 4 است، پس: 16= 42 = 7+5+3+1 ، اكنون بايد عدد وسط 25+ 23+ ... + 7+ 5+ 3+ 1 را پيدا كنيم: 13= 2÷ 26، 26= 25+1 پس حاصل عبارت بالا برابر 132 يا 169 است.
اگر الگويابي را با مسائل زيبا و جالب به دانشآموزان آموزش دهيم زودتر و بهتر مفهوم آن را ياد ميگيرنديكي از فوايد الگويابي و تقويت آن، كشف فرمولها و روابط رياضي مي باشد.
يكي از مسائل زيبا كه مي تواند براي آموزش الگو يابي مفيد باشد ، ضرب عدد 37 در مضربهاي 3 مي باشد . در اين ضربها، الگوهاي زيادي مي توان پيدا كرد كه دانش آموزان را تشويق مي كندتا در منزل دنبال الگوهاي ديگري از اين عدد يا عددهاي ديگر باشند.
4440= 120× 37 3330= 90 × 37 2220= 60 × 37 1110= 30 × 37 111= 3 × 37
4551= 123× 37 3441= 93 × 37 2331= 63 × 37 1221=33× 37 222= 6 × 37
4662= 126× 37 3552= 96 × 37 2442= 66 × 37 1332 = 36 × 37 333= 9 × 37
4773= 129 × 37 3663= 99 × 37 2553= 69 × 37 1443 = 39× 37 444= 12 × 37
4884= 132× 37 3774= 102 × 37 2664= 72 × 37 1554= 42 × 37 555= 15 × 37
4995= 135 × 37 3885= 105 × 37 2775= 75 × 37 1665= 45× 37 666= 18 × 37
5106= 138 × 37 3996= 108× 37 2886= 78 × 37 1776= 48 × 37 777= 21 ×37
5217= 141× 37 4107= 111× 37 2997= 81 × 37 1887= 51 × 37 888= 24 × 37
5328= 144 × 37 4218= 114 × 37 3108= 84× 37 1998= 54× 37 999= 27 × 37
5439= 147× 37 4329= 117× 37 3219= 87× 37 2109= 57× 37
اگر به اين ضربهاي زيبا توجه كنيد ، مي توانيد الگوهاي زيادي پيدا كنيد.
در زير به چند الگو اشاره مي شود كه شما با استفاده از اين الگوها مي توانيد حاصل ضرب را تا هر جايي كه مايل باشيد ادامه دهيد بدون اينكه از ماشين حساب استفاده كنيد.
1. در رديف اول الگوها به اين صورت است كه اگر مضرب بر 3 تقسيم كنيم مي توانيم نتيجه را تشخيص دهيم . به عنوان مثال اگر 37 را در 24 ضرب كنيم ، چون 8 = 3: 24 پس نتيجه 888 مي شود.
2. در رديف دوم ، هم الگو به صورت ستوني و هم رابطه اي با رديف اول دارد.به عنوان مثال در رديف دوم و سو م و چهارم و پنجم ، رقم هاي يكان به صورت عمودي از صفر شروع و به 9 ختم مي شود و همين الاگو نيز در رقم دهگان و صدگان مشاهده مي شود.
3. و چندين الگوي زيباي ديگر كه اگر به دقت به عددها توجه كنيد، اين رابطه ها و الگوها را مشاهده مي كنيد.
4. اگر اين ضربها را به همين ترتيب ادامه دهيد خواهيد ديد كه باز هم اين الگوهارا مشاهده خواهيد كرد.
5. در ستونها ي دوم و سوم و ... ، مجموع رقم يكان و يكان هزاربا رقم تكراري وسط برابر است. به عنوان مثال 1998 = 54 × 37 كه 1+8 با رقم تكراري وسط يعني 9 برابر است.
6. هرگاه رقم وسط بعد از 9 به 10 مي رسد رقم يكان هزار نيز يك واحد اضافه مي شود و اين الگو تا پايان مشاهده مي شود.
2-5- مدلسازي
مدلسازي شبيه كشيدن نقاشي است. با اين ويژگي كه اشيا بهتر از تصاوير مورد استفاده قرار ميگيرد. در پايههاي ابتدايي، بازي با پول براي تمرين داد و ستد و استفاده از مدلهاي ساعت براي فعاليت «خواندن ساعت» به طور مستمر مورد استفاده قرار ميگيرد. از مدلهاي سه بعدي مكعبها و هرمها و اجسام سه بعدي هندسي ديگر در جريان يادگيري اين اشكال استفاده ميشود. مزيت مدلها نسبت به نمودارها اين است كه كودكان ميتوانند در جريان آموزش يك مسأله آن را بررسي و دست به دست كنند. رباتهاي پلاستيكي استفاده شده در خط كش سانتيمتري مسأله در زير و استفاده از صفحات گرد و كاغذهاي 10×10 مدلهاي خوبي براي مسائل 2 و 3 در زير است:
مسأله(1): خط رباتها
پنج ربات در طول خيابان ايستادهاند. «بوكو» 25 متر جلوتر از «روكو» است. «لوكو» 10 متر پشت «بوكو» است. «موكو» 5 متر پشت «لوكو» است «موكو» 15 متر پشت «سوكو» است. رباتها را از چپ به راست رديف كنيد.
مسأله (2): دوچرخه سوارها
صبح يكشنبه 7 دوچرخهسوار و 19 چرخ از كنار خانهي ما عبور كرد. چند دوچرخه و چند سه چرخه از كنار خانه ما عبور كرده است.
مسأله (3): جمعكنندههاي تمبر
«مارسيا» سه برابر برادرش تمبر دارد. اگر برادرش 8 تمبر ديگر داشته باشد، تعداد تمبرهاي آنها برابر خواهد شد. مارسيا چند تمبر دارد؟