الگوها-دنباله ها -عددهاي متوالي2
الگو ها -عددهاي متواليالگو ها-شكل
يكسري عدد در زير داريم:
مثال: 1, 4, 7, 10, 13, 16, 19, ... .
مثال2: 2, 4, 8, 16, 32, ... هربار عددقبلي 2برابرشده يا به عكس
عددهاي الگويي
كاربا اين عددها خيلي شيرين ودلنشين است .مغزرا به جنب وجوش مي اندازد.
عددهاي الگويي ياسري حسابي
عددهاي بعدي با فاصله معين ازهم ادامه دارند: يعني اختلاف هردوجمله متوالي ازيكسري عدد مقدار ثابت باشد. به اين سري عدد تصاعد حسابي گويم وفاصله را قدرنسبت مي گوييم:
مثال:
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
تفاوت بين اين سري با فاصله3واحد است .روي محور فاصله ها 3واحد 3واحد را ببينيد.:


مثال:
| 3, 8, 13, 18, 23, 28, 33, 38, ... |
تفاوت بين اين سري هردوعددبا فاصله5واحد است .روي محور فاصله ها 5واحد 5واحد را ببينيد.:

عددي كه به عددبعدي هربا راضافه شود "اختلاف مشترك"
اختلاف مشترك بين اين سري چه عددي است؟
| 19, 27, 35, 43, ... |
پاسخ:8
اختلاف مشترك مي تواندمنفي باشد.:
مثال:
| 25, 23, 21, 19, 17, 15, ... |
دراين سري هرعدد 2 - شده است.
تصوير راببينيد:
 |
سري هندسي
دريكسريعدديادنباله از جمله دومي به بعد هرجمله مساوي عددثابتي ضرب در عددقبلي.
مثال:
| 2, 4, 8, 16, 32, 64, 128, 256, ... |
اين دنباله، عددبعدي2برابرعددقبلي است.
روي محور نشان داديم:

مثال:
| 3, 9, 27, 81, 243, 729, 2187, ... |
اين دنباله، عددبعدي2برابرعددقبلي است..
درمحورزير ببينيد:

دنباله هاي خاص
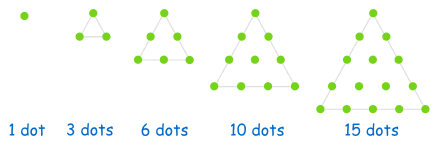
عددهاي مثلثي:مثلثي و ... بنظر شما اين اعداد چه ويژگي مشتركي دارند؟ اگر دست به قلم نشويم و شكل نكشيم و آزمايش نكنيم، فهميدن ارتباط ميان آنها كمي دشوار است. به اين شكل دقت كنيد مشكل شما حل خواهد شد. به اعداد موجود در اين سري، اعداد مثلثي مي گوييم
1 = 1
3= 1+2
6= 1+2+3
10= 1+2+3+4
15= 1+2+3+4+5
21= 1+2+3+4+5+6 .
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
سري اعدامثلثي اولين بار 1000 سال پيش خيام ارائه كرد. و400سال پيش پاسكال باكمكايناعداد،سري ديكري ارائه كردوبه مثلث خيام پاسكال معروف شد.
اولي يك نقطه(دكمه)-دومي 3نقطه(دكمه)-سومي 6 نقطه(دكمه) و................
اگر شمار دكمههاي واقع در يك ضلع مثلث معلوم باشد، تعيين مجموع دكمههاي آن ساده است. كافي خواهدبود، كه آن را با تمام اعداد طبيعي متوالي كوچكتر از خود جمع كنيم. مثلاً اگر تعداد دكمهها در يك ضلع ۵ تا باشد، شماركل دكمهها۱+۲+۳+۴+۵ يعني ۱۵تا خواهدبود.
اعدادمربعي:
| 1 مربع | = | 12 | = | 1 × 1 | = | 1 |
| 2 مربع | = | 22 | = | 2 × 2 | = | 4 |
| 3 مربع | = | 32 | = | 3 × 3 | = | 9 |
| 4 مربع | = | 42 | = | 4 × 4 | = | 16 |
| 5 مربع | = | 52 | = | 5 × 5 | = | 25 |
| 6 مربع | = | 62 | = | 6 × 6 | = | 36 |
| 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
يعني مجذور(مربع) عددهاي حسابي از صفرتا.......:
0 (=0×0)
1 (=1×1)
4 (=2×2)
9 (=3×3)
16 (=4×4)
غيره...
راه دوم:مجموع دو عدد مثلثي متوالي: اگر هر دو عدد پشت سرهم در سري اعداد مثلثي را با هم جمع كنيم حاصل جمع يك عدد مربع مي شود. مثلا" 1+3=4 يا 3+6=9 يا 6+10=16 و ...
مكعب n عددمتوالي
| 3 مكعب | = | 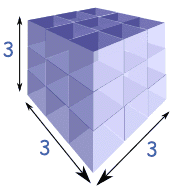 |
= | 3 × 3 × 3 | = | 27 |
مكعب عدد يعني =33
| 4 مكعب | = | 43 | = | 4 × 4 × 4 | = | 64 |
| 5 مكعب | = | 53 | = | 5 × 5 × 5 | = | 125 |
| 6 مكعب | = | 63 | = | 6 × 6 × 6 | = | 216 |
| 1, 8, 27, 64, 125, 216, 343, 512, 729, ... |
1 (=1×1×1)
8 (=2×2×2)
27 (=3×3×3)
64 (=4×4×4)
غيره..
اعدادفيبوناتچي
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... |
غير از دو عدد اول اعداد بعدي از جمع دو عدد قبلي خود بدست ميآيد. اولين اعداد اين سري عبارتاند از:
0+1
2= (1+1) و..............
21=(8+13)
55 (21+34)و....
عددبعدي چيست؟
دنباله هاي تصويري
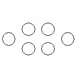
اين تصوير را خودتان الگويابي كنيد: مرحله پنجم چند سكه ؟ قانوني برايش بنويسد:
 |
 |
 |
|
| مرحله=1 | مرحله=2 | مرحله=3 | مرحله=4 |
|---|---|---|---|
| 1 سكه | 6 سكه | 15 سكه | 28 سكه |